Введение
В последние годы был достигнут огромный прогресс в области компьютерного моделирования движения жидкостей. Этот успех связан с развитием и применением различных математических подходов, включая методы конечных разностей, конечных объемов и элементов, а также спектральные методы, которые эволюционировали вместе с увеличением вычислительной мощности компьютеров.
Благодаря более мощным компьютерам, мы теперь способны моделировать всё более сложные процессы движения жидкости с высокой точностью как в пространстве, так и во времени.Применение численного моделирования движения жидкости в области энергетики позволяет эффективно решать задачи, связанные с генерацией, передачей и использованием различных видов энергии.
Однако, даже с современными вычислительными возможностями, традиционные подходы к решению сложных задач все еще сталкиваются с некоторыми проблемами. Например, классические методы требуют разбиения исследуемой области на множество маленьких фрагментов (создания расчетной сетки, см. рис.1), что иногда может быть сложной и неточной операцией, особенно в случае нестандартной формы области

Рис. 1. Пример неравномерной расчетной сетки для двумерной задачи обтекания тела потоком жидкости
Кроме того, следует внимательно подходить к выбору методов приближения вычислений и решений уравнений во времени. Использование разных подходов к одной и той же задаче может существенно повлиять на точность и стабильность решения. Также классические методы часто используют упрощенные условия, которые не всегда точно отражают реальные физические процессы. Они могут недостаточно учитывать шум или неточности в граничных условиях. А для моделирования действительно сложных процессов, таких как турбулентность или некоторые химические реакции, требуется учесть огромное количество переменных, что значительно усложняет вычисления.
Таким образом, некоторые задачи, связанные с движением жидкостей (и не только), требуют такого количества вычислительных ресурсов, что их решение становится практически невозможным. Часть этих проблем может решить суррогатное моделирование, которое становится все более популярным в наше время. Суррогатное моделирование предполагает замену дорогостоящих вычислений более экономичными и быстрыми с помощью приближенных расчетов изучаемой модели. Эти методы позволяют более точно и адаптивно подходить к моделированию движения жидкости и учитывать сложные условия и процессы. Следовательно, они открывают новые горизонты для исследования и предсказания движения жидкости и других процессов.
В последние годы методы машинного обучения и анализа данных становятся все более популярными, предлагая новый подход к решению сложных научных и технических проблем. Благодаря использованию современных вычислительных мощностей, таких как графические процессоры и библиотеки для машинного обучения, машинное обучение открывает новые возможности для исследования, моделирования и прогнозирования движений жидкости.
В контексте умного города применение численного моделирования движения жидкости может быть полезным в различных аспектах. Например, оно может помочь в оптимизации городского водоснабжения и водоотведения, улучшении системы управления дорожным движением и предотвращении наводнений. Кроме того, моделирование движения жидкости может использоваться для прогнозирования последствий изменения климата на городскую инфраструктуру и принятия соответствующих мер.
Лаборатория прикладных цифровых технологий Международного математического центра Новосибирского государственного университета провела исследования в области суррогатного моделирования на основе машинного обучения, и ниже представлены наиболее интересные результаты этой работы.
Предсказание полей обтекания тела потоком жидкости с помощью графовой нейронной сети (GNN)
Гидродинамические вычисления используются для решения сложных математических уравнений, которые описывают движение жидкости и газа. Эти вычисления имеют множество применений, от создания более эффективных промышленных изделий до понимания и прогнозирования изменений климата. Во время разработки новых продуктов необходимо тестировать множество идей, чтобы создать продукт с лучшими характеристиками. В этом помогает суррогатное моделирование - процесс, при котором сложные и длительные испытания заменяются более простыми и быстрыми.
Одним из важных применений суррогатного моделирования является прогнозирование того, как жидкость или газ будут двигаться вокруг определенного объекта. Это важно для создания более эффективных кораблей, самолетов и других движущихся объектов. Однако, чтобы решить эту задачу традиционными методами, требуется огромное количество вычислительных ресурсов. Необходимо провести множество испытаний, чтобы найти оптимальную форму объекта, так как это задача с множеством переменных, и это требует много времени и ресурсов.
Для ускорения процесса можно искать приближенные решения, которые находятся рядом с точными решениями, где уже могут быть найдены точные решения. Этот метод обычно более быстрый и эффективный. Вместо того чтобы искать точные решения “с нуля”, суррогатное моделирование позволяет быстро найти решения, близкие к идеальным, и затем использовать более точные численные методы для их уточнения
Как упоминалось ранее, сейчас нейросети часто используются в качестве суррогат-моделей. В последнее время по этой теме было проведено множество исследований, и большинство из них использовали сверточные нейросети (CNN). Например, в одном из исследований CNN использовалась для решения уравнения Пуассона, которое описывает движение жидкостей и газов. Этот метод значительно ускоряет моделирование физических процессов. Другие исследования использовали CNN для предсказания полей скорости и давления, определяя скорость и направление движения жидкости в любой точке пространства. Это возможно благодаря использованию двумерных сеток и дополнительной информации о каждой точке, такой как координаты, расстояние от границ и другие параметры.
Однако использование CNN имеет один существенный недостаток - низкая точность предсказаний вблизи границ объектов, поскольку эта технология работает только с регулярными сетками, которые дают более низкое разрешение в областях с высокой плотностью точек.
Графовые нейросети использовались для предсказания полей течения в ряде исследований. В этих работах сеть обучалась на основе точных решений и предсказывала решения на основе структуры нерегулярных сеток и информации, содержащейся в их узлах (координатах, индикаторах границ). Таким образом, графовые нейросети находят широкое применение в задачах, связанных с гидродинамикой, и позволяют достигать хороших результатов.
В нашем исследовании мы более подробно изучили применение графовых нейросетей для задачи обтекания. Здесь погруженное тело и форма входного потока могут изменяться. Схематичное представление этой задачи показано на рисунке 2.
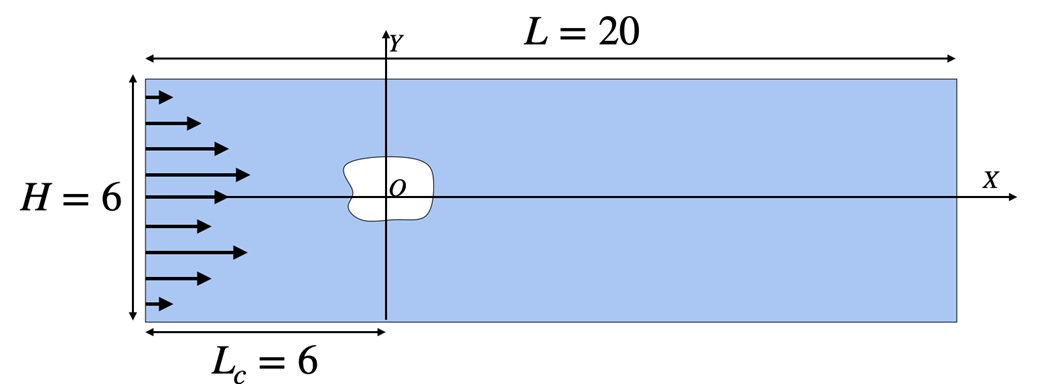
Рис. 2. Схема задачи предсказания полей обтекания тела потоком жидкости
Для обучения графовой нейросети был использовались метод прямого численного моделирования, который генерирует обучающие данные из тысяч различных решений. Форма погруженного тела и скорость горизонтального потока на входе в канал задаются несколькими параметрами, выбранными случайным образом в допустимом диапазоне для каждого решения.
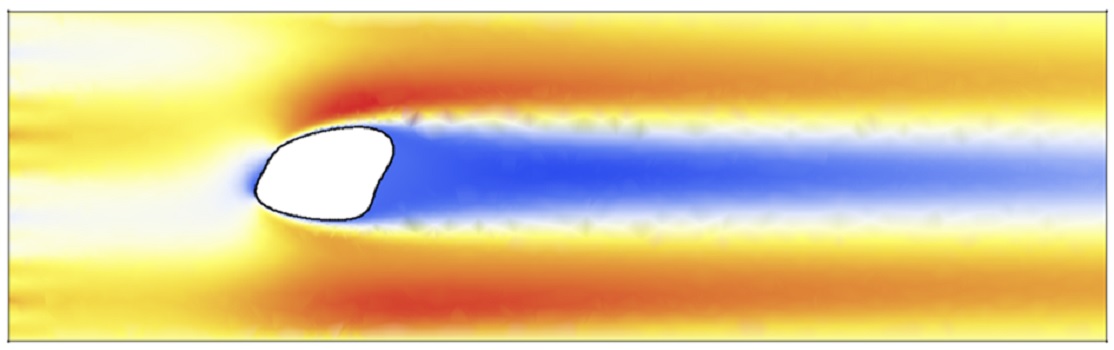
Рис. 3. Пример поля горизонтальной скорости течения обтекания тела
Особенностью графовых нейросетей является то, что они делают предсказания на основе пространственных данных из определенной области. Однако, в данной задаче граничные условия могут быть переменными, поэтому важно учесть практически всю область расчета.
В ходе нашего исследования мы предложили новую модификацию архитектуры графовых нейросетей, которая позволяет увеличить рецептивное поле и повысить точность предсказаний в задачах обтекания с варьируемыми параметрами. Ключевым отличием этой архитектуры является использование параметризации граничных условий, описываемой небольшим набором чисел, а также механизма учета глобальной информации из области расчета (рис. 4).
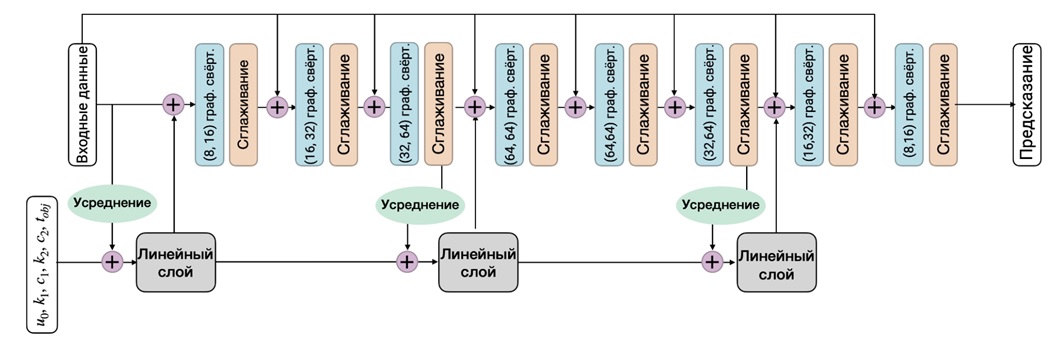
Рис. 4. Модифицированная модель
На рисунке 5 представлено сравнение ошибок предсказания с помощью стандартной GNN и с нашей модификацией, на нем можно увидеть, что общая ошибка уменьшилась в ~2 раза и пропали аномальные области.
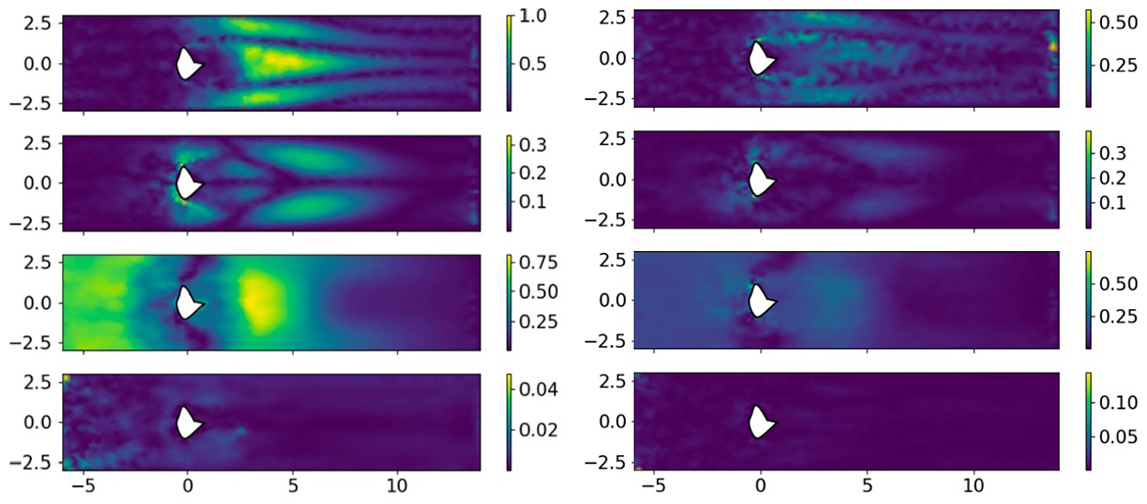
Рис. 5. Сравнение ошибок предсказания с помощью стандартной GNN и с нашей модификацией
Графовые нейронные сети представляют собой перспективный подход для проведения исследований. Их ключевое преимущество заключается в способности создавать достаточно точные решения для задач с изменяемой геометрией расчетной области. В настоящее время набирает популярность метод PINN, который вносит информацию о физических процессах в процесс обучения модели. Этот метод может существенно улучшить работу модели, сократить размер обучающей выборки и повысить точность.
Нейронные сети, основанные на физике (PINN)
Одним из революционных подходов, выделяющихся среди нейросетевых методов, стал метод, появившийся в 2017 году. Он позволяет работать непосредственно с уравнениями, описывающими течение жидкости, без использования точных данных или сеток, и получил название PINN (“physics-informed neural networks”, нейронные сети с физической информацией). Интерес к этому подходу в последнее время возрастает, и число научных публикаций, его использующих, с каждым годом увеличивается.
Метод PINN позволяет интегрировать знания о физических процессах в обучение нейросетей, делая его мощным инструментом для исследования и анализа движения жидкостей. Он объединяет физическую интуицию с преимуществами современных методов машинного обучения для более точного и эффективного решения задач этой области. PINN использует нейросети для моделирования физических процессов, учитывая при этом уравнения, описывающие эти процессы, путем интеграции уравнений и граничных условий.
Таким образом, метод PINN обладает следующими преимуществами:
Метод PINN позволяет включать физическую информацию в обучение нейросетей, делая его эффективным инструментом для анализа движения жидкостей. Его преимуществами являются:
- Интеграция физической интуиции и уравнений в модель для повышения точности.
- Гибкость: подходит для решения различных задач.
- Не требует точных данных, можно использовать при неполной информации.
- Способен решать сложные задачи, включая моделирование турбулентных течений, химических реакций, процессов в теплопередачи и оптимизацию энергосистем.
- Применяется для моделирования процессов в энергетике и оптимизации энергосистем.
- Обучение нейросетей на современных вычислительных ресурсах ускоряет процесс моделирования.
С течением времени популярность метода PINN растет, и он находит широкое применение в различных областях, таких как аэродинамика, гидродинамика, медицинская диагностика и других. Однако, поскольку методология PINN только начинает развиваться, есть много аспектов, которые еще не изучены, и вопросов, на которые нет ответов. Один из них - определение наиболее эффективных инструментов и стратегий использования этой технологии в зависимости от типа уравнений и конкретной задачи. Кроме того, есть неопределенность в отношении наилучших конфигураций нейросетей, которые могут успешно применяться в различных ситуациях. Поскольку универсального подхода к выбору лучших методов и техник для различных уравнений и задач не существует, определение оптимальных путей решения проблем затруднено. В настоящее время не существует единой системы рекомендаций или стандартизированных процедур. Важно отметить, что в настоящее время нет единого программного решения, которое могло бы охватить все разнообразие необходимых инструментов и возможностей для работы с этим методом.
В связи с этими ограничениями наша работа направлена не только на исследование и оптимизацию методов и инструментов для метода PINN, но и на разработку собственного программного обеспечения.
Наши цели включают в себя:
- Создание универсального и гибкого программного комплекса, который поможет исследователям и инженерам решать различные задачи, связанные с PINN, и настраивать его под свои потребности и условия.
- Проведение исследования различных инструментов в контексте PINN и разработка подробного руководства, показывающего, какие из этих инструментов могут быть более или менее эффективными для работы с различными типами уравнений.
Мы успешно разработали первую версию нашего программного комплекса, основываясь на идеях универсальности и гибкости. В основе этого комплекса лежит фундаментальная идея – он способен эффективно решать системы уравнений, независимо от их размера или порядка (универсальность). Наша архитектура разработана с учетом легкости интеграции новых инструментов (гибкость), что делает наш продукт просто неотъемлемым для разнообразных математических задач.
На текущий момент наш программный комплекс способен решать любые системы уравнений, вне зависимости от их порядка или сложности. Он уже содержит различные модельные и тестовые уравнения и демонстрирует впечатляющие результаты при решении сложных задач. Рисунок 6 показывает два примера успешного использования нашего комплекса для решения разных задач. Важно отметить, что решения сходятся к ожидаемым результатам, и комплекс с легкостью справляется как с трехмерными, так и с двумерными задачами.
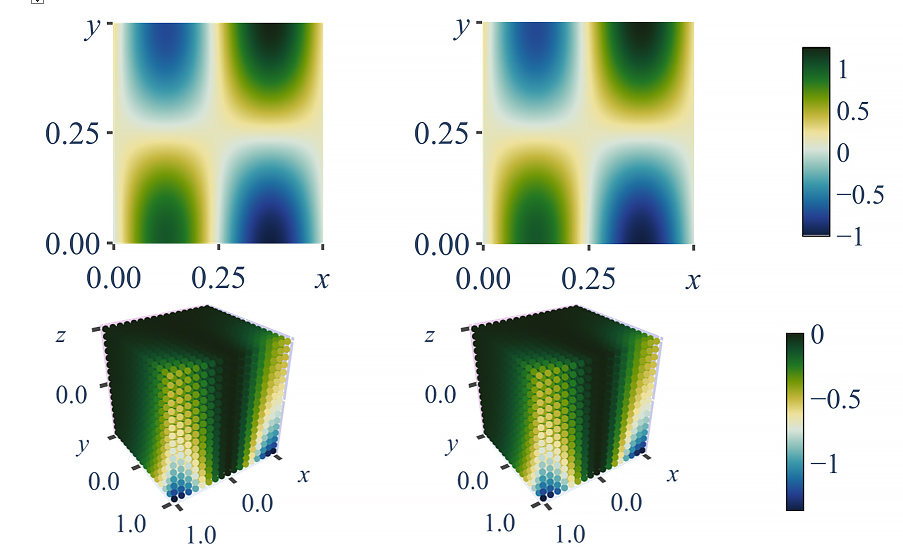
Рис. 6. Точное и численно найденное решения для двух различных задач (по строкам). Слева – решения, полученные с использование разработанного пакета PINN, справа – точное решение
Мы также успешно интегрировали ряд популярных и исследуемых инструментов, дополняющих возможности нашего программного комплекса:
- Адаптивные сетки. Эта функция позволяет определить области с наибольшей неопределенностью и автоматически увеличивать объем обучающих данных в них. Это повышает эффективность обучения нейросети, позволяя ей адаптироваться к сложным данным.
- Регуляционные члены. Мы предоставляем возможность использования статических и адаптивных регуляционных членов. Они улучшают сходимость метода, балансируя обучение в соответствии с значимостью различных частей данных.
- Различные нейросетевые архитектуры. Наши пользователи могут выбирать из двух основных типов архитектуры: полносвязные и с обходными путями. Мы также исследовали и внедрили специализированные архитектуры, такие как сверточные сети и рекуррентные нейронные сети.
В настоящее время продолжается разработка программного комплекса для PINN и исследование имеющихся и новых инструментов для решения уравнений в этой технологии. Этот метод имеет большой потенциал для использования в моделировании различных процессов в сфере энергетики, где необходимо эффективное решение уравнений для анализа и предсказания поведения систем.
В контексте умного города использование технологии PINN может предложить новые решения для оптимизации работы различных городских систем, таких как энергетика, транспорт, водоснабжение и т.д. Она может помочь в прогнозировании поведения систем и предотвращении возможных проблем, что в итоге приведет к улучшению качества жизни горожан.
Список литературы:
- Sharma P. et al. A Review of Physics-Informed Machine Learning in Fluid Mechanics // Energies. – 2023. – Т. 16. – №. 5. – С. 2343.
- Tompson Jonathan, Schlachter Kristofer, Sprechmann Pablo, and Perlin Ken. Accelerating eulerian fluid simulation with convolutional networks // International Conference on Machine Learning / PMLR. –– 2017. –– P. 3424–3433.
- Guo Xiaoxiao, Li Wei, and Iorio Francesco. Convolutional neural networks for steady flow approximation // Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. –– 2016. –– P. 481–490.
- Ribeiro Mateus Dias, Rehman Abdul, Ahmed Sheraz, and Dengel Andreas. DeepCFD: Efficient steady-state laminar flow approximation with deep convolutional neural networks // arXiv preprint arXiv:2004.08826. –– 2020.
- Eichinger Matthias, Heinlein Alexander, and Klawonn Axel. Stationary flow predictions using convolutional neural networks // Numerical Mathematics and Advanced Applications ENUMATH 2019: European Conference, Egmond aan Zee, The Netherlands, September 30-October 4 / Springer. –– 2020. –– P. 541–549.
- Chen Junfeng, Hachem Elie, and Viquerat Jonathan. Graph neural networks for laminar flow prediction around random two-dimensional shapes // Physics of Fluids. –– 2021. –– Vol. 33, no. 12. –– P. 123607.
- Yang Zhishuang, Dong Yidao, Deng Xiaogang, and Zhang Laiping. AMGNET: multi- scale graph neural networks for flow field prediction // Connection Science. –– 2022. –– Vol. 34, no. 1. –– P. 2500–2519.
- Kashefi Ali, Rempe Davis, and Guibas Leonidas J. A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries // Physics of Fluids. –– 2021. –– Vol. 33, no. 2. –– P. 027104.
- He Xiaodong, Wang Yinan, and Li Juan. Flow completion network: Inferring the fluid dynamics from incomplete flow information using graph neural networks // Physics of Fluids. –– 2022. –– Vol. 34, no. 8. –– P. 087114.
- Karniadakis G. E. et al. Physics-informed machine learning //Nature Reviews Physics. – 2021. – Т. 3. – №. 6. – С. 422-440.
- Penwarden M. et al. A unified scalable framework for causal sweeping strategies for Physics-Informed Neural Networks (PINNs) and their temporal decompositions //arXiv preprint arXiv:2302.14227. – 2023.
- Wu C. et al. A comprehensive study of non-adaptive and residual-based adaptive sampling for physics-informed neural networks //Computer Methods in Applied Mechanics and Engineering. – 2023. – Т. 403. – С. 115671.
- Wang S., Teng Y., Perdikaris P. Understanding and mitigating gradient pathologies in physics-informed neural networks //arXiv preprint arXiv:2001.04536. – 2020.
- Sitzmann V. et al. Implicit neural representations with periodic activation functions //Advances in neural information processing systems. – 2020. – Т. 33. – С. 7462-7473.